Ultrasonic testing (UT) important formulas & Calculations

One of the key aspects of UT is the use of formulas to calculate various parameters related to the inspection process. These formulas are essential for determining factors such as material thickness, defect size, wave velocity, and attenuation. In this article, we will explore some of the most important UT formulas and how they are applied in practice.

UT requires specialized equipment and skilled technicians who are proficient in interpreting the data obtained from these tests. However, a thorough understanding of the important formulas and calculations involved in ultrasonic testing can help technicians analyze and interpret test results accurately.

For basic of Ultrasonic testing, check out this post:

Ultrasonic Testing of Weld

UT Frequency

Frequency is the number of cycle per second and denoted by ‘f’. The unit of frequency is Hertz (Hz). Higher units are KHz and MHz.

1Hz = 1 cycle/second
1 KHz = 1000 Hz

1 Mhz = 1000 KHz or 1000000 Hz.

The frequency (f) can be represented by following equation:

f = 1/T, where T is time. or,

T = 1/f

Ultrasonic Wavelength & Velocity

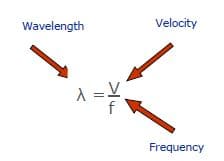
The speed of sound wave transmission from one point to other by the soundwave motion is called the sound velocity. The formula for UT wave velocity (V) is:

Velocity = Distance/ time or V = λ/T, replacing the T with equation given earlier (T = 1/f) in this equation, we will have:

V = λf or
λ = V/f

Velocity Calculation: The velocity of ultrasound in a material can be calculated using the formula: Velocity = Distance / Time.

Example Caluclation:

What will be the wavelength of 400Hz frequency sound passing in air?

λ = V/f, or λ= 332/400 = 0.83m

Note: 332 is the speed of sound in air in m/second.

Ultrasonic Velocity Chart

Signal amplitude Calculation

The amplitude of an ultrasonic signal is the maximum displacement of molecules from their equilibrium position, while the energy of the signal is represented by the square of its amplitude. The relative amplitude of ultrasonic signals is measured using decibels (dB), a logarithmic unit of comparison.

When comparing the height of two signals on a CRT screen, we are essentially comparing the electric voltage sent to the Y plates, which is proportional to the square of the current. To compare two signals, we need to use a formula that considers this relationship.

Difference in dB = 20 x Log₁₀ H1/H2
For example, if we want to compare a signal of 40mm with one of 20mm on the
CRT screen:

Difference in dB = 20 x Log₁₀ (40)/(10), = 20Log₁₀ 2
Find the log₁₀ of 2 in tables or a calculator.
= 20 x 0.301 = 6.02dB

Velocity of different types of Sound waves

The main types of ultrasonic testing sound waves are:

Longitudinal waves or also called compression wave. The velocity of Longitudinal waves, Velocity V(L) is highest.
Shear waves or also called Transverse waves. Velocity of shear waves, Velocity V(T) is almost half of the V(L) waves.
Rayleigh waves or Surface waves. Velocity of surface waves, Velocity V(S) is around 90% of V(T).

Plate waves or Lamb Waves: Only travel is solid materials.

Relationship between different types of sound waves:

Velocity V(L) = 50% Velocity V(T)
Velocity VS) = 90% Velocity V(T)

Near Zone/ Near Field Calculation in Ultrasonic Testing

The near zone of a crystal varies with the material being tested, but it can be
worked out by a formula:

Near Zone or Near Field = D²/4λ, or

D²f/4v (since λ = V/f, as we see earlier)

Here, ‘D‘ is dia of crystal, ‘f‘ is sound frequency, ‘λ‘ is wavelength and ‘V‘ is Velocity of sound in the material. So, greater the D or crystal diameter, bigger the near zone as well as higher frequency means higher near zone.

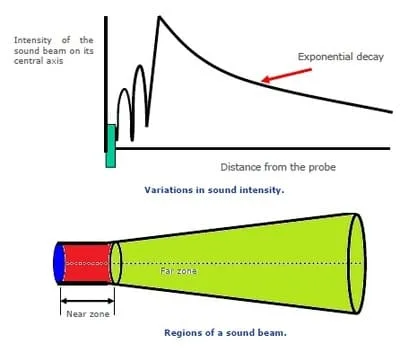
So, to have a small near zone, either choose small diameter crystal or use low frequency.

Example Calculation: What will be the near zone of 2 MHz longitudinal prove of 20 mm crystal diameter in steel?

Near Zone = (20² x 2000000)/(4 x 5920000) = 33.8 mm (using the formula, Near zone= D²f/4v)

Here, 20 is crystal diameter, 2000000 is frequency in Hz and 5920000 is sound velocity in steel in mm/second.

Calculation for Normal Incidence at an interface

Reflection factor, R = (Z₁-Z₂)²/(Z₁+Z₂)²

Transmission factor, T= (4Z₁Z₂)/(Z₁+Z₂)²

Calculation for Oblique Incidence

In case of a UT beam is incident at an angle to the interface, then the reflected wave is also at an angle to the surface. Here, as per Snell’s Law:

Sin I/ Sin R = V₁/V₂

If we want to make a probe transmitting a shear wave at a certain angle, we
have to transpose the formula:

Sin I = (Sin R V₁)/V₂

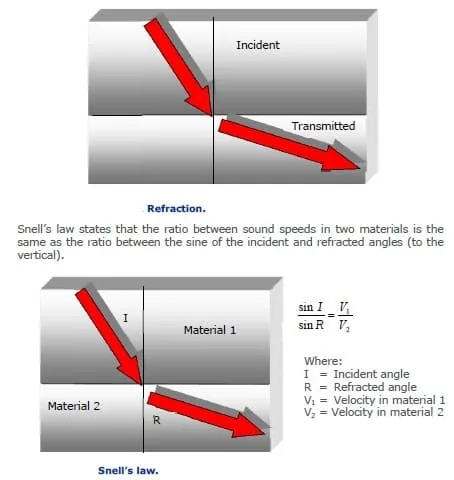
Example Calculation:

To illustrate, when aiming for a 45-degree shear wave in steel using a probe, we need to determine the incident angle by calculating the appropriate angle to cut the Perspex wedge. The speed of sound in compression within Perspex is 2730 m/s, while the speed of sound in shear within steel is 3250 m/s. Our desired refracted angle is 45 degrees.

Sin I – (Sin 45^o x 2730)/3250
Sin I – (0.7071x 2730)/3250

Sin I = 0.594
I = 36.44^o

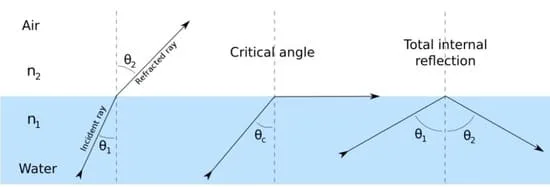
Critical Angle Calculation

Snell’s law is applicable for determining critical angles in non-ferrous metals. In the case of immersion scanning, where water serves as the incident material, a different set of angles needs to be calculated. The initial critical angle refers to the incident angle at which the compression wave is generated in the test material at 90 degrees. So using Snell’s law:

Sin I/Sin 90^o = 2730/5960
Sin90^o = 1
Sin I = 2730/5960

The second critical angle is the incident angle at which a shear wave is
generated in the material at 90^o. Use Snell’s law again:

Sin I/Sin 90^o = (2730 m/s)/(3240 m/s)
Sin I = 2730/3240

Sin = 0.8245
I = 57.4^o

Additional formulas:

Snell’s Law: Snell’s Law is used to calculate the angle of refraction when ultrasound waves pass through a boundary between two materials with different velocities. It is given by: sin(theta1) / sin(theta2) = Velocity1 / Velocity2

Wavelength Calculation: The wavelength of an ultrasound wave can be calculated using the formula: Wavelength = Velocity / Frequency
Attenuation Calculation: Attenuation refers to the reduction in the amplitude or energy of ultrasound waves as they propagate through a material. It can be calculated using the formula: Attenuation (dB) = 20 * log10 (Initial Amplitude / Final Amplitude)
Thickness Measurement: UT is commonly used for measuring the thickness of materials. The formula for thickness measurement is: Thickness = (Velocity * Time) / 2

Beam Spread Calculation: Beam spread refers to the widening of the ultrasound beam as it propagates through a material. It can be calculated using the formula: Beam Spread = (Wavelength * Distance) / Beam Diameter